What is the relationship from an inscribed angle to its intercepted arc?
At that place are 2 very of import relationships between angles and intercepted arcs in circles. The first one is about key angles and their intercepted arcs.
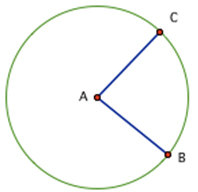
Angle BAC is a central angle with intercepted arc CB. The measure out of the fundamental angle equals the measure out of its intercepted arc.
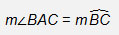
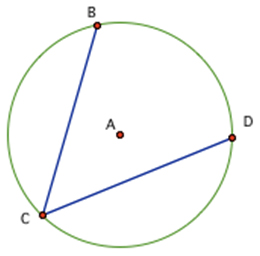
The second relationship is most inscribed angles and their intercepted arcs.
Angle BCD is an inscribed angle with its intercepted arc BD. The measure out of the inscribed bending is half the measure of the intercepted arc.
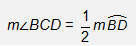
What happens if an inscribed angle and a key angle intercept the aforementioned arc on a circle?
Apply the interactive below to investigate the relationship between ∠ABC, an inscribed angle, and ∠ADC, a central angle, that both intercept 
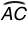. Click the START button to begin the animation. As the animation progresses, expect for patterns in the ii angle measures.
What relationship practice you notice betwixt the measure of an inscribed angle and the measure out of a fundamental bending if they intercept the same arc on a circle?
Interactive popup. Assistance may be required.
Interactive popup. Assistance may exist required.
When you make a theorize from patterns that you detect, you are using inductive reasoning to make your conjecture. You tin can use deductive reasoning to show that your conjecture is truthful every time.
In the interactive below, drag the reason that best supports the statement in the flow proof of a conjecture that could be made from observing patterns in measures of inscribed angles and key angles that intercept the aforementioned arc on a circle.
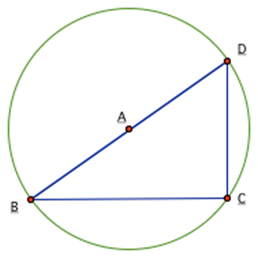
Suppose y'all have an inscribed bending whose sides get through the endpoints of a diameter. In other words, the inscribed angle is included in a semicircle. What conjecture can you make about this angle? Let'due south investigate.
| Example ane | Instance ii |
| | |
| Look at instance 1. What exercise y'all find? | Look at example ii. Does the relationship you noticed in example i concord for angles E and F? (Hint: Apply the corner of a piece of paper to cheque.) |
In your notes, complete the following conjecture and then click on the blanks to bank check your answer.
Inscribed angles in a Interactive button. Assistance may be required. _______________ semicircle are always Interactive button. Assistance may be required. _______________ correct angles.
The conjecture that y'all simply made is based on inductive reasoning. Y'all can use deductive reasoning to show that your conjecture is always true.
In the interactive below, drag the reason that best supports the statement in the menses proof of a conjecture that could exist fabricated from observing patterns in measures angles that are inscribed in semicircles.
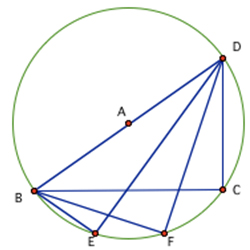
Let'south await at some other situation where we take inscribed angles that share the same intercepted arc simply are not necessarily correct angles.
Click on the start push button beneath to compare two inscribed angles that share the same intercepted arc.
In the interactive beneath, drag the reason that all-time supports the statement in the menses proof of a conjecture regarding the congruency of inscribed angles that share a common intercepted arc.
Intermission and Reflect
How does using deductive reasoning to prove a conjecture relate to using a step-by-stride idea process?
Interactive popup. Assistance may be required.
Practise
Use circle J, shown below, to answer questions one-3.
- Jaime used a protractor to mensurate ∠DCE to be 37°. He ended that m
was 74°. What theorem or postulate supports his conclusion? Interactive popup. Assistance may be required.
- Kathleen used a protractor to measure ∠DCE to be 37°. She ended that m∠DFE = 37°. What theorem or postulate supports her conclusion?
Interactive popup. Help may be required.
- If chiliad∠DCE = 37°, what is 1000∠DJE? State the relationships that you used to decide the angle measure out.
Interactive popup. Assistance may be required.
Interactive popup. Assistance may exist required.
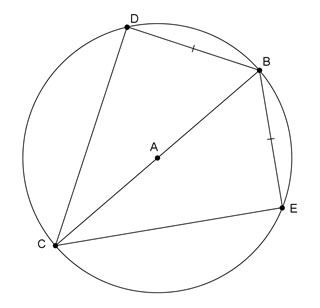
- What is m∠CDB? How practise y'all know?
Interactive popup. Help may exist required.
Interactive popup. Assistance may exist required.
- Regina used a protractor to measure ∠DBC to be 52°. She concluded that g∠DCB = 38°. What theorems or postulates support her conclusion?
Interactive popup. Assistance may exist required.
Interactive popup. Assistance may be required.
Use circle A, shown below, to answer questions 4 and 5.
Source: https://www.ontrack-media.net/gateway/geometry/g_gm1l19rs2.html
0 Response to "What is the relationship from an inscribed angle to its intercepted arc?"
Postar um comentário